¿Quien fue boole?
¿Para que sirve el algebra de boole?


Álgebra de Boole (también llamada álgebra booleana) en informática y matemática, es una estructura algebraica que esquematiza las operaciones lógicas Y, O, NO y SI (AND, OR, NOT, IF), así como el conjunto de operaciones unión, intersección y complemento.
Se denomina así en honor a George Boole (2 de noviembre de 1815 a 8 de diciembre de 1864), matemático inglés autodidacta, que fue el primero en definirla como parte de un sistema lógico, inicialmente en un pequeño folleto: The Mathematical Analysis of Logic, publicado en 1847, en respuesta a una controversia en curso entre Augustus De Morgan y sir William Rowan Hamilton. El álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional. Más tarde fue extendido como un libro más importante: An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities (también conocido como An Investigation of the Laws of Thought o simplemente The Laws of Thought ), publicado en 1854.
En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico. Claude Shannon fue el primero en aplicarla en el diseño de circuitos de conmutación eléctrica biestables, en 1948. Esta lógica se puede aplicar a dos campos:
- Al análisis, porque es una forma concreta de describir como funcionan los circuitos.
- Al diseño, ya que teniendo una función aplicamos dicha álgebra, para poder desarrollar una implementación de la función.
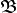 formado cuando menos por los elementos:
formado cuando menos por los elementos: 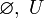 en el que se ha definido:
en el que se ha definido:- Una operación unaria interna, que llamaremos complemento:
- La operación binaria interna, que llamaremos suma:
- La operación binaria interna, que llamaremos producto:
Dada la definición del álgebra de Boole como una estructura algebraica genérica, según el caso concreto de que se trate, la simbología y los nombres de las operaciones pueden variar.

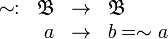



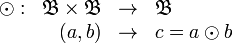

No hay comentarios:
Publicar un comentario